这个百年数学问题被隔离在家的数学家破解了

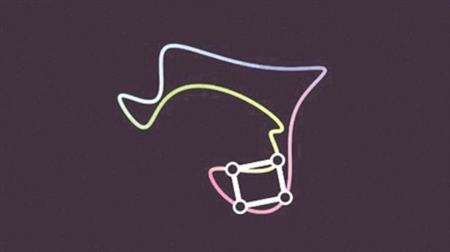3月中旬，数学家乔舒亚·格林和安德鲁·洛布发现自己处于这样的窘境：疫情期间，他们被困在家里。因此，他们决定全身心投入到研究中来解决这个问题——— 是否总能在任何一个简单闭合环路上找到四个点，形成一个任意长宽比矩形？

这个问题，被称为内接方形问题（或方形钉问题），源自1911年。100多年来，数学家们一直在致力于解决它。当时，德国数学家奥托·托普利兹预测称，任何简单闭合曲线，都包含四个可以连接形成正方形的点——— 这听上去像是个高中生能用尺子解决的问题。

华盛顿与李大学助理教授伊丽莎白·丹内感叹称：“这个问题说出来很容易，也很容易理解，但想要证明真的很难。”

在这个过程中，数学家们给出的解题思路，也成为后继者实现突破的阶梯。

在1977年，数学家赫伯特·沃恩首先在内接矩形问题上取得了突破，开创了一种思考矩形的几何形状的新思路。

另一位数学家陶哲轩，则用积分方法证明了，在曲线由两个常数小于1的Lipschitz图形组成的这种特殊情况下，该曲线一定存在四个能组成正方形的点。

对于平面上的任意简单闭合环路而言，矩形的存在已经得到了证明，但是否任意长宽比的矩形（包括正方形）都能存在，此前的数学家们都没能解决。

而格林和洛布在疫情期间，基于赫伯特·沃恩的方法，将这个问题彻底解决了。证明的思路是：如果证明了存在任意长宽比的内接矩形，那么方形（长宽1∶1的矩形）也必然是存在的。而且这一结论比陶哲轩想要证明的内接方形结论更强。

新闻推荐

默克尔：美若不承担全球性大国责任，欧洲需重估同其关系

新华社柏林6月27日电（记者张远任珂）据德国《南德意志报》27日报道，德国总理默克尔说，美国如果不愿承担全球性大国责任，欧...